 Textbook Material
Textbook Material
 Read the following materials
Read the following materials
 Programming Material
Programming Material
 Simple Programming Exercises Do these problems as soon as possible.
Simple Programming Exercises Do these problems as soon as possible.
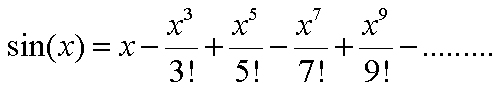
Using the more efficient EXP(X) program as an example, write a program that implements the sine function with the above infinite series. Test your program with small numbers (e.g., 3.14, -6, 10) as well as large numbers (e.g., 5000, 10000, 1234567, -98765, 9999999, -9998887). What are the results? Anything wrong? Keep in mind that the function value of sine is in [-1,1].
Second, since the sine function has a period of 2PI, where PI = 3.1415926....., we may rewrite this program to take advantage of this fact. More precisely, y = MOD (x, 2*PI) yields the same result as x does. In other words, we have sin(x) = sin(y) = sin(MOD (x, 2*PI)). In this way, a large x is reduced to a small number in [0,2*PI).
We may go further. Since sin(x + PI) = -sin(x), x can be reduced to [0,PI). In the last step, the range of x has been reduced to [0,2*PI). If x >= PI, we have sin(x) = -sin(x - PI), where x - PI is in [0,PI), a small number between 0 and 3.14159... Note that you can obtain PI easily and accurately with cos-1(-1).
Now, rewrite your sine program in which the input x is made non-negative and reduced to the range [0,PI). Then, use the same set of large numbers to testing this new version. Would this new version be better in terms of accuracy and trouble free?
 Do the following problems
Do the following problems
 From our text
From our text
 Additional Practice Problems Do these problems as our class proceeds
in this week.
Additional Practice Problems Do these problems as our class proceeds
in this week.
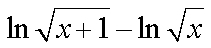
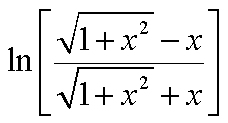
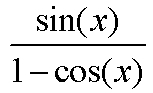
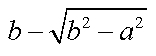
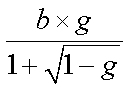
 Food for Thought
Food for Thought
 This is an interesting but somewhat more difficult problem.
Do it whenever it is possible (before Exam 1 will take place).
This is an interesting but somewhat more difficult problem.
Do it whenever it is possible (before Exam 1 will take place).
|
Let us consider a dramatic floating-point computation experiment.
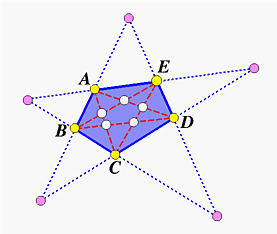
The above shows a pentagon ABCDE. If we draw the five diagonals of this pentagon, we have a smaller pentagon inside the pentagon ABCDE. This smaller pentagon has its vertices in white color. Let us call the original pentagon P and the smaller pentagon in(P), because it is the result of "going" inside of pentagon P. If we extend the sides of the given pentagon, they will intersect in five points, which define a new pentagon outside of the pentagon P. We call this new "outside" pentagon out(P), because it lies outside of pentagon P. From this construction, we know that going out from in(P) should be P. Similarly, going in from out(P) should also be P. More precisely, we have P = out(in(P)) and P = in(out(P)). Let ink(P) denote executing the "going in" operation k times, and let outk(P) denote executing the "going out" operation k times. Then, the following should hold
This means that going in k times followed by going out k times should yield pentagon P. Similarly, going out k times followed by going in k times should also yield pentagon P. Now consider the following strange pentagon:
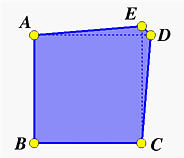
The vertices are as follows, where p is a very small value (e.g., 0.00005).
Would the following operations still hold for very small p? What would be the main reason or reasons that can make the following false?
|
| You do not have to turn in your paper. What I really expect you to do is using these problems to gauge your understanding of the subject. So, do the problems after finish reading the above sections. |