Programming Assignment III

Due on Monday, November 2, 2020 @ 11pm

50 points

This is a warm-up simple multithreaded programming assignment using ThreadMentor.

The Prefix Sum Problem

Given a sequence of n integers x0, x1, x2, ..., xn-1, the prefix sum of this sequence is another sequence
       y0 = x0,
       y1 = y0 + x1 = x0 + x1,
       y2 = y1 + x2 = x0 + x1 + x2,
       ...
       yn-1 = yn-2 + xn-1 = x0 + x1 + ... + xn-1.
For example, if the sequence contains the following five numbers: 1, 5, 3, 6, 8, the prefix sum is 1, 6 = 1+5, 9 = 1+5+3, 15 = 1+5+3+6, 23 = 1+5+3+6+8. This is a very simple problem and can be solved as follows: 

y[0] = x[0];
for (i = 1; i < n; i++)
     y[i] = y[i-1] + x[i];
Or, if we wish to compute the prefix sum in the same array, it is simply: 
for (i = 1; i < n; i++)
     x[i] = x[i-1] + x[i];
The total number of additions is n-1, and this is an O(n) algorithm.

How could the prefix sum be computed in a concurrent way? Well, we do not have the proper synchronization mechanism to solve this problem so far. But, we still can solve this problem in an inefficient way with all the correct ideas in place.

For simplicity, we will assume that the number of integers is always a power of 2. That is, n = 2k for some k > 0. In other words, k = log2(n).

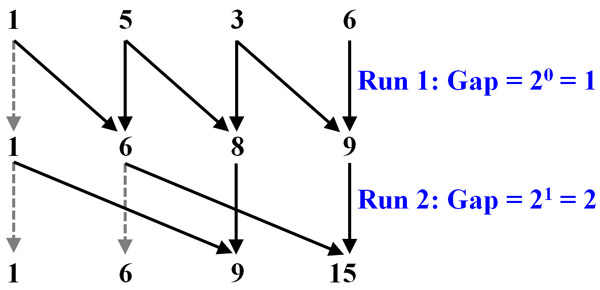
Consider a sequence of four integers: 1, 5, 3 and 6. In this case, we have n = 4 = 22 (i.e., n = 4 and k = 2). For four numbers (n = 4), it takes 2 (k = 2) runs to complete the work. The first run calculates the sum of two adjacent numbers (i.e., the gap between two numbers being 20 = 1). Thus, the resulting sequence is 1, 6 = 1+5, 8=5+3, 9=3+6. The second run calculates the sum of two numbers that are 2 positions away (i.e., gap = 21). From the result of the first run 1, 6, 8, 9, the result of the second run is 1 (copied), 6 (copied), 9=1+8, 15=9+6. The following is a diagram showing the computation process. This diagram uses solid arrows to indicate the additions and light color arrows for copying.

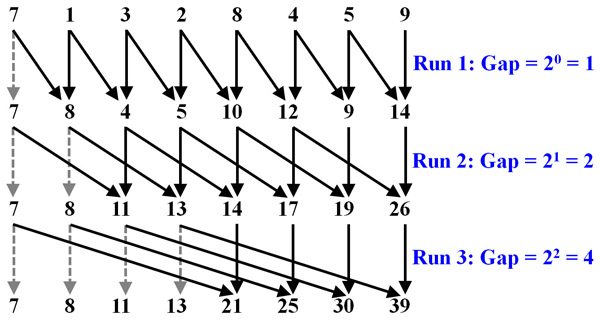
Now consider a sequence of 8 numbers: 7, 1, 3, 2, 8, 4, 5, 9 (i.e., n = 8 and k = log2(8) = 3). This takes three runs to complete the prefix sum. The gaps are 1 = 20 for the first run, 2 = 21 for the second run, and 4 = 22 for the third run. For the first run, we use the adjacent elements, yielding 7, 8=7+1, 4=1+3, 5=3+2, 10=2+8, 12=8+4, 9=4+5, 14=5+9. For the second run, the gap is 2 = 21 and we have 7 (copied), 8 (copied), 11=7+4, 13=8+5, 14=4+10, 17=5+12, 19=10+9, 26=12+14. For the third run, the gap is 4 = 22 and the final result is 7 (copied), 8 (copied), 11 (copied), 13 (copied), 21=7+14, 25=8+17, 30=11+19, 39=13+26. The diagram below shows the details of this process

In general, if we have n = 2k numbers, k runs are needed to complete the prefix sum computation. The following is a possible sequential algorithm: 

for (stage = 1, gap = 1; stage <= k; stage++, gap *= 2) {
     for (i = 0; i < n-1; i++) {
          if (i - gap < 0)
               x[i] = x[i];
          else
               x[i] += x[i-gap];
     }
}
Note that the inner loop has some copy operations which can be eliminated completely as shown below: 
for (stage = 1, gap = 1; stage <= k; stage++, gap *= 2) {
     for (i = gap; i < n-1; i++) {
          x[i] += x[i-gap];
     }
}
How many additions are there in the above algorithm? Note that run 1 uses gap 1 = 20, run 2 uses gap 2 = 21, run 3 uses gap 4 = 22, etc. In general, run h uses gap 2h-1. Moreover, if the gap is 2h-1, then the first 2h-1 elements in the array are not used, and the number of additions is n - 2h-1. Because there are k runs in total, where n = 2k, the total number of additions used is
(n - 20) + (n - 21) + (n - 22) + ... + (n - 2k-1)
Rearranging the terms, we have
k×n - (20 + 21 + 22 + ... + 2k-1)
The second part is a geometric progression, which can be computed as follows:
20 + 21 + 22 + ... + 2k-1 = (2k-1)/(2-1) = 2k-1
Therefore, the total number of additions is k×n - 2k + 1. Because n = 2k and k = log2(n), the total number of additions is nlog2(n) - n + 1, and we have an O(nlog2(n)) algorithm. This is slower than the simple O(n) algorithm discussed at the beginning of this page. The major advantage of this slower version is that it can be made concurrent!

Making the Prefix Sum Computation Concurrent!

For run h, we need to execute n-2h-1 additions, one addition per pair of elements that are 2h away. Then, why don't we assign a CPU/thread for each pair? This is exactly what we should do. We could create n threads T0, T1, T2, ...., Tn-1. Thread Ti computes the value of xi + xi-2h-1 for run h. This is shown in the diagram below:

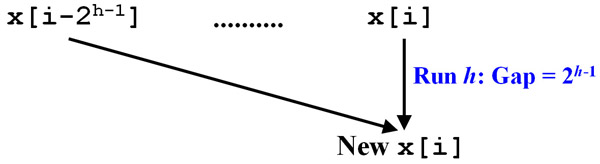
Can the new value of xi be stored back to xi? The answer is NO! (Why?) To overcome this problem, we need another array to store the intermediate results. The array to be used is a 2-dimensional one of k+1 rows and n columns, where k = log2(n): B[k,n]. Initially, we have the input elements stored in row 0 of B[0,*] (i.e., B[0,i] = xi for i = 0, 1, 2, 3, ..., n-1). Then, in run h, n threads T0, T1, T2, ...., Tn-1 are created so that thread Ti computes xi + xi - 2h-1, stores the result in B[h,i], and exits. In this way, the last row of B[k,*] contains the prefix sum results, where k = log2(n) is the number of needed runs.

The Algorithm:

From the above, we are able to quickly develop an algorithm to do a concurrent prefix sum computation. It is summarized as follows:

  1. Suppose the input array x[*] has n = 2k numbers.
  2. Prepare an array B[*,*] of k+1 rows and n columns.
  3. Initialize the 0-th row of B[*,*] so that it contains the numbers of the input array x[*]. More precisely, B[0,j] = x[j] for j = 0, 1, 2, ..., n-1.
  4. Iterate k times (i.e., i = 1, 2, 3, ..., k). For iteration i, do the following:
    1. Create n threads T0, T1, T2, ..., Tn-1.
    2. If j-2i-1 is less than 0, thread Tj simply copies B[i-1,j] to B[i,j]. Otherwise, thread Tj computes B[i-1,j] + B[i-1,j-2i-1] and saves the result to B[i,j].
    3. After this, thread Tj terminates.
  5. After all k iterations complete, the desired prefix sum is on the k-th row of array B[k,*]
You do not have to create n threads in every iteration. We do it in that way because we do not have the needed mechanism yet. Ignoring the repeated thread creation process, we are able to use n threads, each of which iterates k = log2(n) times, to compute the prefix sum of n numbers. If each thread is considered as a CPU, this algorithm means that we are able to use n CPUs to compute the prefix sum of n numbers, and each CPU only iterates k = log2(n) times (i.e., O(log2(n))). This is fast because O(log2(n)) is faster than O(n). For example, if we have 1024 = 210 numbers, the sequential algorithm requires 1024-1 = 1023 additions on a single CPU while the concurrent one requires 1024 CPUs each of which executes only 10 = log2(1024) additions!

Program Specification

Write a program (i.e., the main) to read in n integers into the array x[*], and initialize the array B[*,*] by copying x[*] to the 0-th row of B[*,*]. Then, iterates k = log2(n) times. In each iteration, the main creates n threads as discussed in the previous section and waits for all n threads to exit. Finally, the main prints out the last (i.e., k-th) row of array B[k,*].

Here are a few notes:

Input and Output

The input to your program should be taken from stdin. Your executable must be named as prog3. The command line looks like the following, where input-filename is a file from which prog3 reads in the input values: 

./prog3 < input-filename
The input file has the following format, where n is an integer of form 2k for some integer k > 0, and x0, x1, ..., xn-1, are n integers. You may assume all input values are correct so that you do not have to do error checking. 

n
x0  x1  x2 ...  xn-1

Suppose the command line is 

./prog3 < in.txt
and the file in.txt has the following lines: 
8
7 1 3 2 8 4 5 9
Click here for a copy of this file.

Then, your program output should look like the following: 

Concurrent Prefix Sum Computation                 // from main()

Number of input data = 8                          // from main()
Input array:                                      // from main()
   7   1   3   2   8   4   5   9                  // from main()
                                                  // each number occupies 4 positions
                                                  // there has to be k = log2(n) runs 
                                                  // from main(), do it for each run
Run i:                                            // from main(), run i
     ..........
     Thread j Created                             // from thread j
     ..........
     Thread j computes x[j] + x[j-2^(i-1)]        // from thread j
                                                  // thread j fills in the values of 
                                                  //     j and j-2^(i-1) 
                                                  //     fill in the values of j and j-2^(i-1)
     Thread j copies x[j]                         // thread j copies if no computation needed 
     ..........
     Thread j exits                               // thread j exits
     ..........
Result after run i:                               // from main()
  aa bb cc dd ee ff gg hh                         // from main()
                                                  // use the input array format

Final result after run k:                         // from main()
   7   8  11  13  21  25  30  39                  // from main()
                                                  // use the input array format

In the above sample output, the main() prints out the input and all intermediate result arrays. The main() iterates k = log2(n) times. Iteration i uses gap length 2i-1, where i = 1, 2, ..., k. Thus, the gaps are 1, 2, 4, 8, 16, ..., log2(n)-1. All lines printed by the main() starts on column 1, and each data value is printed with 4 positions.

In each iteration, main() creates n threads, each of which does the following: (1) prints a message indicates that it has been created, (2) prints the two entries this threads has to add (e.g., x[5]+x[3] for run 2), and (3) terminates. All output from a thread starts on column 6.

Submission Guidelines

General Rules

  1. All programs must be written in C++.
  2. Use the submit command to submit your work. You can submit as many times as you want, but only the last on-time one will be graded.
  3. Unix filename is case sensitive, THREAD.cpp, Thread.CPP, thread.CPP, etc are not acceptable.
  4. We will use the following approach to compile and test your programs: 
    make               <-- make your program
./prog3 < in.txt   <-- test your program
    This procedure may be repeated a number of times with different input files to see if your program works correctly.
  5. Your implementation should fulfill the program specifications as stated. Any deviation from the specification will cause you to receive zero point.
  6. A README file is always required.
  7. No late submission will be graded.
  8. Programs submitted to wrong class and/or wrong section will not be graded.

Compiling and Running Your Programs

This is about the way of compiling and running your program. If we cannot compile your program due to syntax errors, wrong file names, etc, we cannot test your program, and, as a result, you receive 0 point. If your program compiles successfully but fails to run, we cannot test your program, and, again, you receive 0 point. Therefore, before submitting your work, make sure your program can compile and run properly.
  1. Not-compile programs receive 0 point. By not-compile, I mean any reason that could cause an unsuccessful compilation, including missing files, incorrect filenames, syntax errors in your programs, and so on. Double check your files before you submit, since I will not change your program. Note again: Unix filenames are case sensitive.
  2. Compile-but-not-run programs receive 0 point. Compile-but-not-run usually means you have attempted to solve the problem to some degree but you failed to make it working properly.
  3. A meaningless or vague program receives 0 point even though it compiles successfully. This usually means your program does not solve the problem but serves as a placeholder or template just making it to compile and run.

Program Style and Documentation

This section is about program style and documentation.
  1. For each file, the first piece should be a program header to identify yourself like this: 
    // ----------------------------------------------------------- 
// NAME : John Smith                         User ID: xxxxxxxx 
// DUE DATE : mm/dd/yyyy                                       
// PROGRAM ASSIGNMENT #                                        
// FILE NAME : xxxx.yyyy.zzzz (your unix file name)            
// PROGRAM PURPOSE :                                           
//    A couple of lines describing your program briefly        
// -----------------------------------------------------------

    Here, User ID is the one you use to login. It is not your social security number nor your M number.

    For each function in your program, include a simple description like this: 

    // ----------------------------------------------------------- 
// FUNCTION  xxyyzz : (function name)                          
//     the purpose of this function                            
// PARAMETER USAGE :                                           
//    a list of all parameters and their meaning               
// FUNCTION CALLED :                                           
//    a list of functions that are called by this one          
// -----------------------------------------------------------
  2. Your programs must contain enough concise and to-the-point comments. Do not write a novel!
  3. Your program should have good indentation.
  4. Do not use global variables!

Program Specifications

Your program must follow exactly the requirements of this programming assignment. Otherwise, you receive 0 point even though your program runs and produces correct output. The following is a list of potential problems.
  1. Your program does not use the indicated algorithms/methods to solve this problem.
  2. Your program does not follow the structure given in the specifications. For example, your program is not divided into functions and files, etc when the specification says you should.
  3. Any other significant violation of the given program specifications.
  4. Incorrect output format. This will cost you some points depending on how serious the violations are. The grader will make a decision. Hence, carefully check your program output against the required one.
  5. Your program does not achieve the goal of maximum parallelism.

Program Correctness

If your program compiles and runs, we will check its correctness. We normally run your program with several sets of input data, one posted on this programming assignment page (the public one) and the others prepared by the grader (the private ones). You program must deliver correct results for all data sets. Depending on the seriousness of the problem(s), significant deduction may be applied. For example, if your program delivers all wrong results for the public data set, you receive 0 point for that component.

The README File

A file named README is required to answer the following questions:
  1. Question: Are there any race conditions in this prefix sum computation? Why?
  2. Question: Prove rigorously that this algorithm does compute the prefix sum correctly.
  3. Question: Can the result of x[i]+x[i-2h-1] of run h be saved back to x[i]? Explain your findings as clearly as possible.
  4. Question: The main() creates n threads in each iteration and wait for them to complete. There is a significant amount of time in creating and joining threads. If you are allowed to use extra variables/arrays and busy waiting, can you just create n threads and let them do all the work without the use of a temporary array B[*,*]? Suggest a solution and discuss its correctness.

You should elaborate your answer and provide details. When answering the above questions, make sure each answer starts with a new line and have the question number (e.g., Question X:) clearly shown. Separate two answers with a blank line.

Note that the file name has to be README rather than readme or Readme. Note also that there is no filename extension, which means filename such as README.TXT is NOT acceptable.

README must be a plain text file. We do not accept files produced by any word processor. Moreover, watch for very long lines. More precisely, limit the length of each line to no more than 80 characters with the Return/Enter key for line separation. Missing this file, submitting non-text file, file with long lines, or providing incorrect and/or vague answers will cost you many points. Suggestion: Use a Unix text editor to prepare your README rather than a word processor.

Final Notes

  1. Your submission should include the following files: Note also that without following this file structure your program is likely to fall into the compile-but-not-run category, and, as a result, you may get low grade. Therefore, before submission, check if you have the proper file structure and a correct makefile. Note also that, although visualization is not needed in your submission, you must use it in your program development because visualization is a part of Exam 2 and the Final.
  2. Always start early, because I will not grant any extension if your home machine, network connection, your phone line or the department machines crash in the last minute.
  3. Since the rules are all clearly stated, no leniency will be given and none of the above conditions is negotiable. So, if you have anything in doubt, please ask for clarification.
  4. Click here to see how your program will be graded.