Exercise 2
| Number of Points | 100 |
| Due Date | Friday, October 7, 2005 |

| Number of Points | 100 |
| Due Date | Friday, October 7, 2005 |

Do the following problems:


|

|

|

|
If the shadow of U in MTU is not vertical in your image, you risk lower grade.
You do not have to start from scratch. Check here to get more information and an initial copy of a POV-Ray file.
A more elegant design (i.e., color, texture, simplicity, good-looking objects and so on) will receive a higher grade. Up to 10 bonus points will be given to a creative design. Also make sure that your modified object is clearly shown in the ray-traced image.
You do not have to write all functions. In fact, I have provided you with all necessary tools except for reading and displaying. Click here to download this package (Exer-2.tar.gz). After unzip and untar (see below), you can make it with one of the four makefiles. The executable will be named as render. Run it and you will see the following on screen:
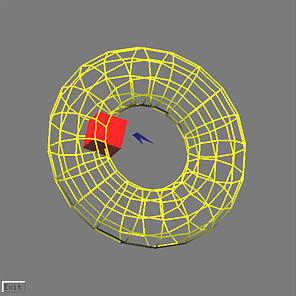
It displays a wireframed torus, a cube and two triangles. You can drag using the left-mouse button to change the orientation of these objects. Click the Exit button to quit this program.
System Notes
You will see four makefiles, each of which is designed to
generate an executable under a particular platform.
Makefile.SunMesa compiles the program without using OpenGL hardware. Makefile.SunOpenGL compiles the system using Sun's OpenGL library. The generated executable runs much faster. Makefile.Linux is for you to compile your program under Linux with Mesa. Finally, Makefile.SGI is for me to grade your program. To make this system, say using Makefile.SunMesa, issue the following command:
|
You only need to modify two functions of this package. Both of them are in file draw.c. The first function is cs390_init(), which is called only once when this program is executed and takes two arguments: argc and argv. See the template below:
void cs390_init(int argc, char **argv)
{
}
In this function, you should read in the input data file whose name
is passed to this function via
argv.
For example, if this program is started with the following line:
then it should read in the winged-edge data structure from file tetrahedron.dat.render tetrahedron.dat
The second function is cs390_draw(). In this function, you should draw the polyhedron read in by function cs390_init(). Obviously, the winged-edge data structure must be global in some way for both functions to have access to it.
While cs390_draw() uses several OpenGL function calls, you only need to know the following:
GLdouble point[3] = { 10.0, 5.0, 20.0 };
.........
glVertex3dv(point);
Note that
glVertex3dv()
requires its only argument
to be a pointer to a array of type
GLdouble.
for (i = 0; i < No_of_Faces; i++) {
glBegin(GL_POLYGON);
for (each vertex of this face) {
glVertex3dv(address of this vertex);
}
glEnd();
}
For each face in the winged-edge data structure,
your program should locate all of its vertices in some
(i.e., clockwise or counterclockwise) order.
Then, for each vertex, use
glVertex3dv() to
send this vertex to OpenGL for further processing.
glBegin(GL_POLYGON) tells OpenGL that a polygon is about to be constructed and glEnd() tells OpenGL that the polygon construction is completed. Between glBegin() and glEnd(), you should supply the vertices in order. Note that these vertices should form a simple (i.e., no self-intersection), planar and convex polygon. Otherwise, the result is unpredictable.
Function glPolygonMode() can be used to draw the edges. For example, the above code can be modified to draw all edges of a face:
for (i = 0; i < No_of_Faces; i++) {
glPolygonMode(GL_FRONT_AND_BACK, GL_LINE); // added!!!
glBegin(GL_POLYGON);
for (each vertex of this face) {
glVertex3dv(address of this vertex);
}
glEnd();
}
The added line instructs OpenGL to draw an outlined polygon.
More precisely, only the edges are drawn. You have two
more choices:
GL_POINT only
draws the vertices of a polygon, and
GL_FILL draws
the polygon filled with a previous specified color.
In cs390_draw(), you should specify a color for your drawing, followed by a loop for displaying the vertices of each face. You should also display all edges of the given polyhedron in a color different from that of the polygons.
Important Notes
|
The result is a file with name Exer-2.tar.gz. Only tar the files. Moreover, remove all .o files and render. If you tar a directory and/or include the .o and render files, you risk lower grade.tar cvf Exer-2.tar file-1 file-2 file-3 ...... gzip Exer-2.tar
It starts with the number of vertices followed by that number of lines, each of which contains the coordinates of a vertex. The next section is a vertex table. Each entry of a vertex table contains an incident edge. A vertex table is followed by a face table. Each entry of a face table contains an incident edge. Finally, it is an edge table. Each entry contains a start and end vertices, left and right faces, the predecessor and successor in a left traverse and the predecessor and successor in a right traverse. The coordinate values of vertices are all in the range of -50 and 50.#V <-------------- number of vertices x y z <-------------- coordinates of the first vertex x y z <-------------- coordinates of the second vertex ....... x y z <-------------- coordinates of the last vertex e <-------------- vertex table: 1st vertex on edge e f <-------------- 2nd vertex on edge f ....... k <-------------- last vertex on edge k #F <-------------- number of faces e <-------------- face table : first face has edge e f <-------------- second face has edge f ....... t <-------------- last face has edge t #E <-------------- number of edges X Y Fl Fr Left-Pred Left-Succ Right-Pred Right-Succ .......
The following is an example which is a translation of the tetrahedron discussed in the winged-edge data structure:
This file is available in Exer-2.tar.gz with name test-0.dat.4 // four vertices 50.0 0.0 5.0 // vertex 1 = A -50.0 50.0 -50.0 // vertex 2 = B -50.0 -50.0 -50.0 // vertex 3 = C 0.0 0.0 50.0 // vertex 4 = D 1 // vertex 1 has edge 1 2 // vertex 2 has edge 2 4 // vertex 3 has edge 4 5 // vertex 4 has edge 5 4 // number of faces 1 // face 1 has edge 1 3 // face 2 has edge 3 1 // face 3 has edge 1 2 // face 4 has edge 2 6 // number of edges 1 4 3 1 5 6 2 3 // edge 1 starts @ v1 & ends @ v4 ... 1 2 1 4 3 1 6 4 // edge 2 2 4 1 2 1 2 4 5 // edge 3 2 3 2 4 5 3 2 6 // edge 4 3 4 2 3 3 4 6 1 // edge 5 1 3 4 3 4 2 1 5 // edge 6
If you need a working program and other files for your testing, click here to learn more. Note that these files are for your reference only, you should not submit them as your work. Otherwise, you will receive no credit for this problem.
NAME: your name E-MAIL: your e-mail address EXERCISE: 2 FILES: README, and other files submitted along with README
Program files and scene files should have sufficient details for me to understand your work. Apply all you have learned in programming courses to your programs and scene files.