Exercise 3
| Number of Points | 100 |
| Due Date | Tuesday, October 25, 2005, before class (Problems 1 and 2) Tuesday, October 25, 2005, 11pm |

| Number of Points | 100 |
| Due Date | Tuesday, October 25, 2005, before class (Problems 1 and 2) Tuesday, October 25, 2005, 11pm |

Please do the following problems. Problems 1 and 2 should be on paper, and Problem 3 via e-mail. Windows version is expected.
f(u) = ( cos(u + PI/2), -(1 + sin(u + PI/2)), 0 )where both u and v are in the range of 0 and PI. Note that circular arcs f(u) and g(v) lie on the xy- and xz-coordinate planes, respectively. Analyze the continuity at the origin. More precisely, are f(u) and g(v) C1, C2, G1 or G2 at the origin f(PI) = g(0) = (0,0,0)? Are they curvature continuous?
g(v) = ( -cos(v + PI/2), 0, 1 - sin(v + PI/2) )
You do not have to write all functions. As in the previous exercise, you only need to modify two functions for reading in data and displaying the curve. Click here to download a package for this problem. After unzip and untar (see below), you can make it with one of the four makefiles. The executable will be named as render. Run it and you will see the following on screen:
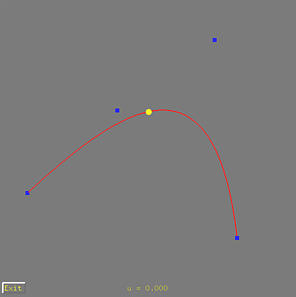
It displays a Bézier curve of degree 3 defined by four control points shown as blue squares and a yellow disk. This yellow disk does not move. It is used as an example. You can click on Exit to close this window and use the left and right arrow keys to change the value of u shown in the middle of the bottom of this window. The range of u is 0 and 1. Press the left-arrow (resp., right-arrow) key to decrease (resp., increase) the value of u.
System Notes
You will see four makefiles, each of which is designed to
generate an executable under a particular system.
Makefile.SunMesa compiles the system without using OpenGL hardware. Makefile.SunOpenGL compiles the system using Sun's OpenGL library. The generated executable runs much faster. Makefile.SunMesa is for you to compile your program under Linux with Mesa. Finally, Makefile.SGI is for me to grade your program. To make this system, say using Makefile.SunMesa, issue the following command:
|
As in the previous exercise, you need to modify cs390_init() to read in a data file whose name is supplied to you with **argv. The file has the following format:
n <------------ degree. number of control points = n+1 x0 y0 z0 <----- 0-th control point x1 y1 z1 <----- 1st control point x2 y2 z2 <----- 2nd control point ...... xn yn zn <----- n-th control point
To draw a Bézier curve, we need to know more about OpenGL. In draw_bezier_curve(), the first for loop puts the control points on screen:
glColor3f(CS390_POINTS_COLOR); /* select a color */
glPointSize(8); /* select the size of a point */
glBegin(GL_POINTS); /* ask OpenGL to show 3d Pts */
for(i = 0; i < n; i++) { /* for each point .... */
glVertex3dv(&points_data[i][0]); /* display it */
}
glEnd(); /* end of point display */
Next, we draw a Bézier curve with the OpenGL function
glEvalCoord1d().
This is the so-called one-dimensional evaluator. In the
following, glEnable()
enables evaluator mapping;
glMap1d() creates a
one-dimensional evaluator, and
glBegin() and
glEnd() ask the
evaluator to generate a sequence of points on the curve and connect
them into a curve, the desired Bézier curve.
glColor3f(CS390_CURVE_COLOR); /* select a drawing color */
glLineWidth(2); /* select a line width */
if(n >= 2) { /* draw curve only if n >= 2 */
glShadeModel(GL_FLAT); /* select a shading model */
glEnable(GL_MAP1_VERTEX_3); /* activate mapping and do it */
glMap1d(GL_MAP1_VERTEX_3, 0.0, 1.0, 3, n, &points_data[0][0]);
glBegin(GL_LINE_STRIP); /* draw a line strip */
for(i = 0; i <= 100; i++) { /* 100 segments */
glEvalCoord1d((GLdouble) (i * 1.0) / 100); /* gen pt*/
}
glEnd(); /* end of line strip */
}
You need to do two things. First, you need to read all
control points into the data array
data[][]. You can
assume there are less than 100 control points. Second, use
glMap1d() to take this
data array as the sixth parameter and
create an evaluator so that when a u is given the evaluator
will generate the corresponding point on the curve.
However, OpenGL does not actually draw a curve. Instead, it requires you to subdivide the domain with many points. Then, OpenGL gets the corresponding points on the curve and joins the adjacent ones with line segments (i.e., line strip). Therefore, if the number of subdivision points is low, the generated Bézier curve looks like a polyline; however, too many subdivision points could slow down your program. In the sample program we use 100. Feel free to modify this value.
The for loop above lets variable i run from 0 to 100. For each i, it is converted to the range of 0 and 1 with (i * 1.0) / 100. This value is sent to glEvalCoord1d(), which in turn will generate a corresponding point on the curve for OpenGL to do the connect-the-dot drawing operation.
Basically, you do not need to change this part at all.
If you look at draw.c carefully, you will see a global double variable u. Each time cs390_draw() is called, a value of u is passed to you with this global variable. The value of u comes from pressing the left- and right-arrow keys.
Here comes your job:
Modify draw.c so that it can display the following:
glBegin(GL_LINE_STRIP);
/* generate a vertex on the polyline */
glVertex3dv(address of this vertex);
/* some other activities */
glEnd();
For a discussion of
glVertex3dv(),
please see Exercise 2.
With a correct implementation, you can drag or rotate the generated Bézier curve and use the left- and right- arrow keys to increase and decrease the value of u. Then, the computation of de Casteljau's algorithm will be shown vividly on screen.
An Important Note |
Here are important notes for this exercise.
NAME: your name E-MAIL: your e-mail address EXERCISE: 3 FILES: README, and other files submitted along with README
SSN is not required.
In your version of Exer-3.tar.gz, in addition to the above sample input, add two more test files input-1.dat and input-2.dat for me to test your program. Each of your test files should contain at least five control points. Interesting curve design will receive up to 5 bonus points. I will also use my own files for testing with the following command:7 -40 -40 -40 -40 40 -40 -40 40 40 -40 -40 40 40 -40 40 40 40 40 40 40 -40 40 -40 -40
render input-file-name
If you need a working program and other files for your testing, click here to learn more. Note that these files are for your reference only, you should not submit them as your work. Otherwise, you will receive no credit for this problem. You can also use DesignMentor to verify your work.